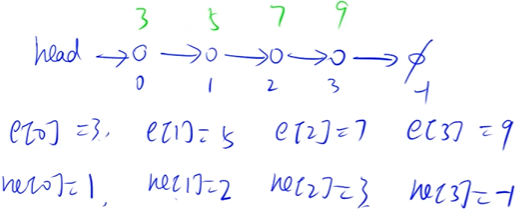链表与邻接表
【一般实现方式:指针+结构体——动态链表(工程中常用)】
1
2
3
4
5
6
7
| struct Node
{
int val;
Node *next;
}
new Node();
|
这里介绍用数组模拟【静态链表】该数据结构的方式——速度快!
单链表
单链表中用的最多的是邻接表——n个单链表:将每个点(共有n个点)的所有邻边存下来
邻接表应用:存储图和树(e.g. 最短路问题、最小生成树问题、……)
单链表基本结构:从头指针开始依次指向若干个节点,每个节点存储一个数值val和一个next指针,沿着next指针不断访问后续数据,直到指向空指针

数组模拟链表存储需要定义(均为整数型数组):
- e[N]:存储各点数值val
- ne[N]:存储各点next指针——空节点下标用-1表示
二者通过下标关联 :
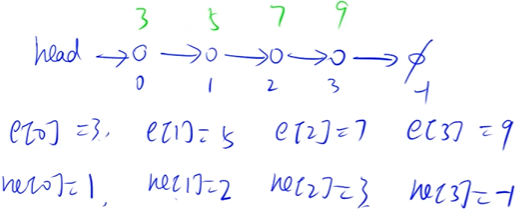
事实上,同一下标i对应的e[i]与ne[i]表示一个节点的数值val及其next指针,将其看作一个结构体会更好理解,但在代码实现过程中,为使得代码尽量简洁,选择直接对数组下标进行操作
1
2
3
4
5
6
7
8
9
10
11
12
|
struct Node
{
int e, ne;
}nodes[N];
void remove(int k)
{
nodes[k].ne = nodes[nodes[k].ne].ne;
}
|
需要注意:一个下标代表一个节点,各节点之间的指向关系仅由next指针(即ne[i]的值)决定
单链表的性质:顺序(单向)访问——可以在O(1)的时间复杂度内找到指定节点的后一个节点(包括完成插入等操作),但如果要找到指定节点之前的节点,则只能从头指针head开始遍历
例题:826. 单链表 - AcWing题库
实现一个单链表,链表初始为空,支持三种操作:
- 向链表头插入一个数;
- 删除第 k 个插入的数后面的一个数;
- 在第 k 个插入的数后插入一个数。
现在要对该链表进行 M 次操作,进行完所有操作后,从头到尾输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数,则按照插入的时间顺序,这 n 个数依次为:第 1 个插入的数,第 2 个插入的数,…第 n 个插入的数。
输入格式
第一行包含整数 M,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令可能为以下几种:
H x,表示向链表头插入一个数 x。D k,表示删除第 k 个插入的数后面的数(当 k 为 0 时,表示删除头结点)。I k x,表示在第 k 个插入的数后面插入一个数 x(此操作中 k 均大于 0)。
输出格式
共一行,将整个链表从头到尾输出。
数据范围
1≤M≤100000 所有操作保证合法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
| #include <iostream>
using namespace std;
const int N = 100010;
int head, e[N], ne[N], idx;
void init()
{
head = -1;
idx = 0;
}
void add_to_head(int x)
{
e [idx] = x;
ne [idx] = head;
head = idx;
idx ++ ;
}
void add(int k, int x)
{
e [idx] = x;
ne [idx] = ne[k];
ne[k] = idx;
idx ++ ;
}
void remove(int k)
{
ne[k] = ne[ne[k]];
}
int main()
{
int M;
cin >> M;
init();
char flag;
int k, x;
while (M -- )
{
cin >> flag;
if (flag == 'H')
{
cin >> x;
add_to_head(x);
}
else if (flag == 'D')
{
cin >> k;
if (k != 0)
remove(k - 1);
else
head = ne[head];
}
else if (flag == 'I')
{
cin >> k >> x;
add(k - 1, x);
}
}
int ptr = head;
while (ptr != -1)
{
cout << e[ptr] << " ";
ptr = ne[ptr];
}
return 0;
}
|
双链表
用于优化某些问题
基本结构与单链表一致,但每个节点会存储两个指针,一个指向前一个节点,另一个指向后一个节点
每个节点(下标)的指针存储方式:数组ne[] -> 指向前一个节点的指针数组l[] + 指向后一个节点的指针数组r[]
双链表中不再定义头节点head与尾节点tail,而是直接令0号下标对应的节点为head节点、令1号下标对应的节点为tail节点
例题:827. 双链表 - AcWing题库
实现一个双链表,双链表初始为空,支持 5 种操作:
- 在最左侧插入一个数;
- 在最右侧插入一个数;
- 将第 k 个插入的数删除;
- 在第 k 个插入的数左侧插入一个数;
- 在第 k 个插入的数右侧插入一个数
现在要对该链表进行 M 次操作,进行完所有操作后,从左到右输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数,则按照插入的时间顺序,这 n 个数依次为:第 1 个插入的数,第 2 个插入的数,…第 n 个插入的数。
输入格式
第一行包含整数 M,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令可能为以下几种:
L x,表示在链表的最左端插入数 x。R x,表示在链表的最右端插入数 x。D k,表示将第 k 个插入的数删除。IL k x,表示在第 k 个插入的数左侧插入一个数。IR k x,表示在第 k 个插入的数右侧插入一个数。
输出格式
共一行,将整个链表从左到右输出。
数据范围
1≤M≤100000 所有操作保证合法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
| #include <iostream>
using namespace std;
const int N = 100010;
int head, e[N], l[N], r[N], idx;
void init()
{
r[0] = 1;
l[1] = 0;
idx = 2;
}
void add(int k, int x)
{
e[idx] = x;
r[idx] = r[k];
r[k] = idx;
l[idx] = k;
l[r[idx]] = idx;
idx ++ ;
}
void remove(int k)
{
r[l[k]] = r[k];
l[r[k]] = l[k];
}
int main()
{
int M;
cin >> M;
init();
char flag[2];
int k, x;
while (M -- )
{
cin >> flag[0];
if (flag[0] == 'L')
{
cin >> x;
add(0, x);
}
else if (flag[0] == 'R')
{
cin >> x;
add(l[1], x);
}
else if (flag[0] == 'D')
{
cin >> k;
remove(k + 1);
}
else if (flag[0] == 'I')
{
cin >> flag[1];
if (flag[1] == 'R')
{
cin >> k >> x;
add(k + 1, x);
}
else if (flag[1] == 'L')
{
cin >> k >> x;
add(l[k + 1], x);
}
}
}
int ptr = r[0];
while (ptr != 1)
{
cout << e[ptr] << " ";
ptr = r[ptr];
}
return 0;
}
|
栈与队列
【一般实现方式:C++ STL中容器】
这里介绍用数组模拟该数据结构的方式。
栈
先进后出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| const int N = 100010;
int stk[N], tt;
stk[ ++ tt] = x;
tt -- ;
if (tt > 0)
else
stk[tt];
|
队列
先进先出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| const int N = 100010;
int q[N], hh, tt = -1;
q[ ++ tt] = x;
hh ++ ;
if (hh <= tt)
else
q[hh];
|
单调栈
单调队列
KMP